Q: How to calculate/derive secondary parameter EC90 from already fitted Sigmoidal /Emax model (both cases) in the Phoenix language?
A. This can be done by adding a secondary parameter that is calculated from the final estimates for the primary parameters (fixed effects). If EC50 and n are known, a general equation to calculate ECF, where F is any percentage, is ECF = ((F/100-F)^(1/n)*EC50))
For EC90, add the following line to the code to calculate EC90 from the textual Hill Emax model:
secondary(EC90 = ((90/(100-90))^(1/n) * EC50))
The EC90 calculated from this equation will appear in the output worksheet named Secondary.
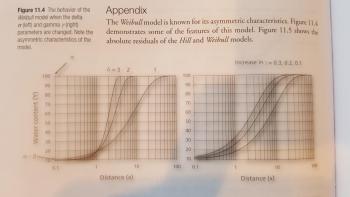
Q: Can we use Weibull model in fitting the data with atypical sigmoidal absorption profile as well?
A: If by atypical you mean asymmetric, then yes the Weibull model can be used for this purpose. The gamma parameter can increase or decrease the X-value of the inflection point, and parameter delta can be used to adjust the steepness of the curve.
Q: Can you explain more about the delta "controls x-value inflection point, how to interprete this value in relation of the dissolution data?
A: See figure 11.4 in PD11, Gabrielsson and Weiner:
Q: Should the difference in log likelihood be weighted against the number of parameters? different degrees of freedom?
A: The Log Likelihood is used in the MLE method to find the maximum likelihood of making the observations given the parameters. The AIC and BIC diagnostics include a penalty for models that have more parameters.
Q: How do you interpret condition number?
A: ‑The condition number is a measure of the stability of the fit. The condition number generally increases as the number of parameters in the model increases. A general rule of thumb is that the condition number should be less than 10^p, where p is the number of parameters in the model. Models with a large condition number may be over-parameterized, meaning that two or more of its parameters are very highly correlated. Consider a reduced model in this case.
Q: Are all of these models nested models? Since we are looking at -2LL...
A: No these are not nested. We can still look to lower -2LL but the differrence is not a chi-sq. May be easier to just use AIC.
Q: Do you show how to use model compare module under phoenix model in one of the webinar?
A: The Model Comparison tool is only available for Population models. This was an Individual modeling example with only one profile, which showed how to implement custom model equations using input data that is not time, concentration, or effect. Data tools were used to select the best model based on plots, diagnostics, and parameter precision. On a side note - the current PML school series (now until August) is focused primarily on Individual Modeling and custom model equations. We are planning a follow-up series to focus on Population Modeling as soon as the first series is complete. If you are interested in Model Comparison tool examples, these are available in both the public and on-demand Intro to Phoenix NLME courses as well as in the Phoenix Help menu.