Hi Nehabatra,
regarding delay statement which I used here:
In the article you sent there is a sentence:
In addition, we introduced a lag time (Tlag) to account for a delayed appearance of the drug in the tumor. The Tlag was estimated by a curve feathering method and subtracted from the time profile of the tumor concentrations.
In PHX6.4 you can use only transit statement (transit compartments) which is closer to the distributed delay. AFAIK there's no common way to get the simple delay in PHX6.4 (maybe some manipulations with sequence? Not sure...)
As I mentioned before this is something new in PHX7 (THX to developers!)
Please follow the PML User's guide for description:
delay( <expression>,<deltaT> )
Outputs the value that <expression> had at the corresponding time in the past (<deltaT>). <deltaT> must be a non-negative expression and can be estimated. If <deltaT> is negative, it is treated as zero, since future values cannot be known.
Delay statements assume an initial value of zero and work by keeping a table of past values of the expression captured at times when the ODE solver was “on trajectory”
(which includes change points like doses) and by using linear interpolation into that table.
If you're interested in delay modeling, please look at the Shuhua Hu's presentation
https://www.youtube....h?v=YCXIW_uxTrs
BR,
Mittyright
Thanks Mittyright.
But still Im not able to write the code in PML as Im facing the problem of incorporating the biexponential equation in the tumor compartment. I need help to write it down and it will be a great help for me.
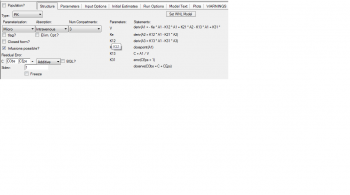
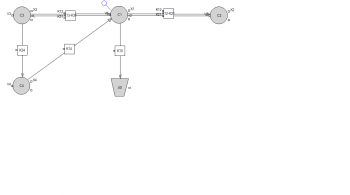
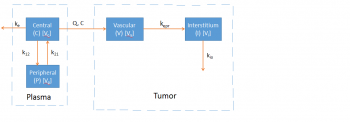
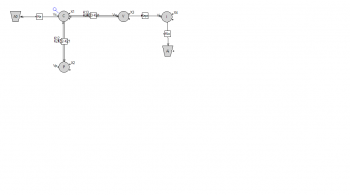
Following you will see the code and and the graphical model has been attached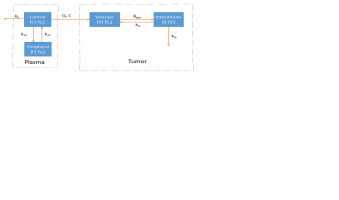
dV/dt = Q * Cp + jiv * I - jvi * V
dI/dt = jvi * V - jiv * I
Cp = A * e^(- a * t) + B * e^(- b * t)
jiv = jvi/s
I = Tumor concentration * Vi
V = Vascular concentration * Vv
s = Vi/Vv
q1.FF = (A*exp(-a*t) + B*exp(-b*t))*fu
flux(2,4) = k(2,4) * q4
k(2,4)=k(4,2)/s
flux(4,2) = k(4,2) * q2
flux(2,1) = k(2,1) * q1
k(2,1)=Q
flux(0,4) = k(0,4) * q4
s1 = q4/(Vv*s)
FF = (A*exp(-a*t) + B*exp(-b*t))*fu
flux(V,I) = k(V,I) * I
k(V,I)=k(I,V)/s
flux(I,V) = k(I,V) * V
flux(V,FF) = k(V,FF) * FF
k(V,FF)=Q
flux(0,I) = k(0,I) * I
s1 = I/(Vv*s)
s1 is the tumor sampling site
For the compartmental model:
dX1/dt = k21 * X2 + k41 * X4 - (k12 + k10 + k13) * X1
dX2/dt = k12 * X1 - k21 * X2
dX3/dt = k13 * X1 - k34 * X3
dX4/dt = k34 * X3 - k41 * X4
flux(1,4) = k(1,4) * q4
flux(4,3) = k(4,3) * q3
flux(3,1) = k(3,1) * q1
flux(2,1) = k(2,1) * q1
flux(1,2) = k(1,2) * q2
flux(0,1) = k(0,1) * q1
ex1.bolus = 0.0
ex1.infusion = 0.0
s5 = q4/v4
s4 = q4/v4
s3 = q4/v4
s2 = q1/v1
s1 = q1/v1
s1 and s2 are sample concentration from central compartment q1 or X1.
s3, s4 and s are smple concentrations from tumor compartment q4 or X4.
Waiting for a reply