Below you will find responses of the Q&A session for this webinar:
Question: In the code, C is drug, what is L?
Answer: L is the ligand – the molecule that binds to another (usually larger) molecule (here the Rx is also the ligand). C is the concentration of the drug.
Question: Can you comment for the TMDD model in the first line of code (PML)? Why are the terms multipled by "V” in the second expression?
Answer: This is because we modeled amounts and not concentrations.
Question: Can you go through the TMDD code line by line to explain each statement? Or at least the important statements that are important for this model?
Answer: see the following (these are the statements other than those defining the initial estimates)
1. deriv(A1 = (-Cl*C -Cld*(C-C2) -(kon*C*R -koff*LR)*V))
the first two terms are for a standard 2 compartment pk model. Note that these two terms are amount (A1), as a clearance times a concentration is amount per time. The next two terms represent the turnover of receptor. Here we have rate constants (kon and koff) times concentrations. We have to multiply these terms by V to get amounts (note that a rate constant times volume is a clearance). In statements 5 and 6 below, we then convert amounts to concentrations which is what is actually measured.
2. deriv(A2 = Cld * (C-C2))
the standard equation for a peripheral compartment
3. deriv(R = kin -kout*R -kon*C*R + koff*LR)
this just expresses the turnover of R in the model
4. deriv(LR = kon*C*R - koff*LR - keRL*LR)
this just expresses the turnover of the complex in the model
5. C = A1/V
6. C2 = A2/Vt
7. kin = R0*kout
the baseline R0 = kin/kout, so kin = R0*kout
8. dosepoint(A1)
this means the mAb was dosed via IV (directly into the plasma)
9. sequence{R = R0}
for any differential equations whose initial state is not zero, we need to define that initial state. Here the initial amount of R is assumed to be R0. We can enter that as a constant (as was done in the example) or we could make it a parameter and estimate it.
Question: Is the R free or total? What if you only measure total R or free R? How to adjust the modeling?
Answer: You could model either, but free is preferred and easier to interpret and scale.
Question: On slide 15, although the CV% decreases, the estimate of the parameter is quite close. In that case, can we assume the model would provide reasonable estimate for amt L?
Answer: For the basic PK related parameters yes (V, V2, Cl, Cld), but not necessarily so for the parameters associated with the receptor and the complex (kon, koff, keLR).
Question: Can you please comment on the Return code and its interpretation and priority?
Answer: The return code is a crude measure of the difficulty the program had in finding the minimum of -2*LL. The best value is 1. If the return code is other than 1, it means that while the program did converge, it had difficulty finding the minimum. The reported -2LL may or may not be the global minimum. When this happens, we suggest you try refitting the data using different initial estimates and see if the program continues to converge to the same value.
Question: We may see nonlinear clearance pattern (bend down and then up) in case of sparse sampling design (mice study) because of variability. How do we verify the TMDD in such cases?
Answer: The nonlinear Cl pattern is a bend down (but not back up). The TMDD pattern is a bend down followed by a bend back up. The ony suggestion we have with sparse sampling is to try to get as many samples in the terminal phase as you can in the same (cohort) of animals and then you could use more random sampling in the other animals (cohorts). This should help discern the TMDD pattern, assuming you are in the right exposure range.
Question: If the mAb does not undergo target binding (target is not expressed in mice), we may not need to consider TMDD but only linear clearance component. How about FCRn mediated clearance in such cases?
Answer: If there is no target mediated clearance, the PK could likely be described by a regular 1, 2, or 3 compartment differential equation model. Even though FcRn recycling is capacity limited, significant alteration in the efficiency of FcRn recycling is not typically achieved with therapeutic doses of mAbs. Worst case scenario (lets say you are dosing 2 g/kg of a mAb), the CL or t1/2 would appear dose dependent.
Question: Do you recommend doing sensitivity analysis for each model?
Answer: there are many types of sensitivity analyses, so I am not sure exactly to what you are referring. But if you have already collected data, and the fitted model CVs are not as good as you would like based on the existing data, and you want to improve the bias and precision in future studies … then yes, sensitivity analyses may help inprove the design (and parameter estimates) for the next trial.
Question: Is it possible to run the presented TMDD model if you don't know the Total Receptor amount (R0 missing)? Any change to the code required?
Answer: Yes, just make R0 a fixed effect and estimate it as a parameter. But of course you will still need an initial estimate for R0.
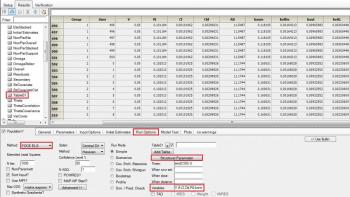
Question: If you have a data set with greater than one subject per dose group, is there a way to obtain secondary parameters for each subject (written in the text mode)?
Answer: Not if you are running in naïve pooled mode. If you are running ELS, then in the Run options specify a Table and click on structural parameters, and you will get a table of individual estimates for each structural parameter. Unfortunately the program still only reports population values for the secondary parameters. The only other thing you could do is refit the model changing the parameterization from (say) Cl to micro, and again request a table of structural parameters.