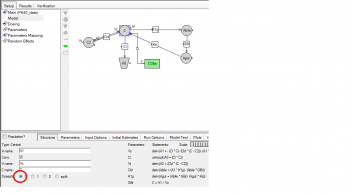
Question: Are you fixing the time for release from gall bladder? Would this not be a parameter to be estimated?
Answer: You are right that we have used a constant value (Ri=10 hours) for the time of release from gall bladder. We did this as it is well defined from the data profile. But one could also estimate this as a parameter
Question: It appears that the model is applied on data from a single subject, can this be done on a population, when the Ri could be different in each subject.
Answer: Yes, even for a single subject one could have estimated Ri as a parameter. In population mode one could also put a random effect on Ri as well.
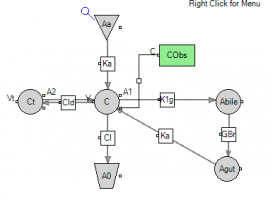
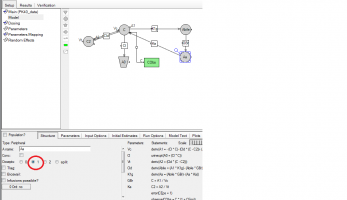
Question: Why did you change C2 to Ct in the modified graphical model?
Answer: This is for notation purposes - C2 is the default name, Ct stands for tissue compartment.
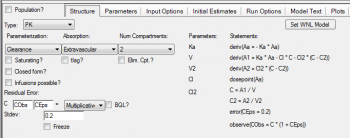
Question: Is the textual model generated automatically from the graphical model?
Answer: Yes, all selections that you make in built-in or graphical mode get written automatically to the model text.
Question: To my understanding you manually need to add the switch variable.
Answer: Correct - the enterohepatic recirculation compartments are added in graphical mode (for convenience) and then the switch is added in Text mode.
Question: In the fixef parameters, what would the third parameter be (after minimum and maximum estimates)?
Answer: The fixef statement asks for a vector with three components as input, the lower bound, the initial estimate and the upper bound, here is an example:
fixef(tV=(lower bound, initial estimate, upper bound))
You can leave the lower and upper bounds blank, since typically the algorithm does not need any boundaries. This is a difference to the legacy PK model engine where boundaries were required.
Question: How do you buildup a model for oral administration instead of IV?
Answer: There are two alternative ways to get to this:
1. Start from built-in options and adjust the settings as we showed in the demo with one exception: choose extravascular as Administration
2. Switch to graphical mode and add the two compartments for bile and gut plus the two flows.
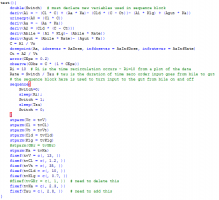
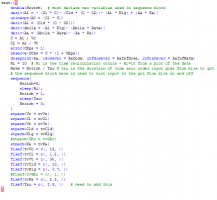
3. Now, switch to textual model and adjust the textual code as we showed in the demo. You need to remove the additional definition for Ka. Here is the model:
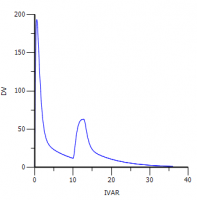
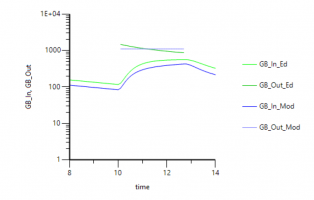
4. When you simulate with the same dose (switched from A1 to Aa) you get the following profile:
Question: If you are simulating an oral dose. Do you create an additional GI compartment for the EHC? Or do you just use the GI compartment that you already have in the model?
Answer: As you can see from answer to the previous question you can have a separate absorption compartment for an oral dose. However, you can use the same GI compartment from our initial model.
Here are the steps:
1. You need to switch back to graphical mode and set the dosepoint in the central compartment to 0
2. Then you add a dosepoint for the GI compartment (renamed to Aa)
3. Finally, you switch to textual model and adjust the model as we did in our demo. The final model text is here:
Question: Would the Ka be different for the absorption of the dose and the absorption of the recycled drug?
Question: Can I apply a second Ka for oral absortion?
Answer: One could try fitting different Ka values (e.g. Ka1, Ka2) for immediate absorption and re-absorption, and then if comparable reduce the model to a single Ka.
Question: For multiple emptying, could you not add more to the switch statement instead of dosing or sin functions?
Answer: Yes, you can add constant cycles to the PML, e.g. like:
Ri = 10 # Ri is the time recirculation occurs - Ri=10 from a plot of the data
Rate = Switch / Tau # tau is the duration of time zero order input goes from bile to gut
EHC_cycle = 5 # assumes an average time interval between food uptake of 5 hours
sequence{
Switch=0;
sleep(Ri);
Switch = 1;
sleep(Tau)
Switch = 0;
sleep(EHC_cyle – Tau)
Switch = 1;
Sleep(Tau)
Switch = 0;
}
Question: Can you simulate gall badder emptying every 24h?
Answer: Yes, typically you would just need to expand the time interval within the sequence block to 24 hours. Here is an example:
Ri = 10 # Ri is the time recirculation occurs - Ri=10 from a plot of the data
Rate = Switch / Tau # tau is the duration of time zero order input goes from bile to gut
sequence{
while(1) {
Switch=0;
sleep(Ri);
Switch = 1;
sleep(Tau)
Switch = 0;
sleep(24 – Ri - Tau)
}
}
I have put a conditional statement into the block since I assume you are thinking about multiple doses. While(1) means: do the loop as long as you have time points in your data set for the specific individual.