6 replies to this topic

[Hellot]

Hi,
after having generated descriptive statistics from several conc-times profiles, when i "sent to" the statistics to XY plot object, i have some standard deviation that disappear for some time points but not for all the groups (even if the values of SD are there in the descriptive stat table/object).
Are there something to be aware of when doing such plots to avoid missing error bars ?
BR,
Edouard

Attached Thumbnails

• 

[Nathan Teuscher]

Edouard,

 

That is very strange. Perhaps you can post a PHX project file with just the summary statistics and the XY Plot to allow us to troubleshoot. My first thought is that there is no SD for certain timepoints (i.e. <2 samples at a given nominal time).

 

Nathan

[Hellot]

Here is the data set of the "blue" data points. I have replaced the BLQ values with the LLOQ and therefore have no missing values and all 6 individuals included in desc stat. here it is strange is that i have four groups and got the problem only with group 3 dataset.
The problem is only on the log scale plot; in the linear plot, the SD are there...Thank you

Attached Thumbnails

• 

[Simon Davis]

Edouard, Please could you post a project illustrating this problem so we can see what mappings etc. are chosen. IF you don't want to post you full current project you could just

 

a) export this worksheet to e.g. CSV

create a new project and import it

c) recreate the plot

d) post the resulting saved project back here.

 

Or even just the worksheet in step a)

 

 Simon.

[Hellot]

Hi and thank you

i have replaced the variable names in the file. [file name=Copy_of_Statistics.xls size=66048]http://pharsight.com/extranet/media/kunena/attachments/legacy/files/Copy_of_Statistics.xls[/file]

Attached Files

•  Copy_of_Statistics.xls   64.5KB   0 downloads

[Simon Davis]

Hi Edouard,
I believe the problem you are observing is an artefact due to the SD being large relative to the mean. This gives a "down" that is a negative value and cannot be represent on a log scale.

I would propose that for this set you select to present only UP error bars, maybe in the future Phoenix could provide a warning of this in the verification notifications and either automatically de-select or suggest to de-select the DOWN mapping for error bars. I will try and get that logged as an enhancement when i get some time.

[Enhancement noted as QC_PHX 12526]

Simon.

Attached Thumbnails

• 

[Helmut Schütz]

Hi Edouard,

I guess Phoenix is giving you an answer to the wrong question. In descriptive statistics generally we estimate the location (the arithmetic, geometric, harmonic means, the median, …) and dispersion (variance, SD, quartiles, percentiles, …) of a sample. No software is “clever” enough to know where your data come from. Therefore, it gives you a lot of information by default (some more options have to be chosen if required) and it is up to you to select the correct ones.

Before applying any (!) statistics you have to think about the data generating process. Then – and only then – you can select the most appropriate parameter(s) describing your data. Note: Any parameter implies knowing the data generating process and the underlying distribution. Example: If you report the arithmetic mean ± SD you essentially tell us “the data were sampled from a normal distribution”. The normal distribution has a domain of definition from [–∞, +∞]. Does this make any sense for concentrations? Obviously not. Like many biologic variables they follow a lognormal distribution, where the domain is ]0, +∞]. In PK I would recommend to simply throw the arithmetic mean into the garbage bin and report statistical parameters relevant for the lognormal, namely the geometric mean and its SD (or CV).

In the setup in PHX tick ”Number of SD”. Send to XY Plot, map GeometricMean to Y, GEOLower1SD to Lower Error Bar and GEOUpper1SD to Upper Error Bar. Select a log Y-scale. Graphs > Error Bars > Content > User Calculation Type: Absolute

Now you’ll get a log-plot with symmetric error-bars. If you want, switch to the linear Y-scale. The error bars will be asymmetric now; exactly what we would expect from a lognormal distribution. BTW, they will never be negative. Try it: Ask PHX for 10SDs. ;-)

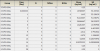
Example:


Below a recent bad example from the FDA (obviously produced by M$-Excel):



That’s plain nonsense. Do these “experts” (ha!) really expect (and this is what the arithmetic mean –SD suggests) that there is a ~6% chance to have a concentration of – (minus!) 300 ng/mL?

If somebody insists on arithmetic means of concentrations, ask them: Why? …and post the answer here, please. I’m always eager to learn something new.